So it turns out the stars don’t revolve around us…

We are bounded in a nutshell of Infinite Space: Worksheet # 3, Problem #2: So it turns out the stars don’t revolve around us…

The Local Sidereal Time (LST) is the right ascension that is at the meridian right now. LST = 0:00 is at noon on the Vernal Equinox (the time when the Sun is on the meridian March 20th, for 2013 and 2014).

a) What is the LST at midnight on the Vernal Equinox?

b) What is the LST 24 hours later (after midnight in part ’a’)?

c) What is the LST right now (to the nearest hour)?

d) What will the LST be tonight at midnight (to the nearest hour)?

e) What LST will it be at Sunset on your birthday?

As I am sure many (and I sincerely hope all) of you have convinced yourself the Earth revolves around the Sun, and the Earth is indeed a near-sphere-like object, we’ll skip over this portion (that being said, if you want to learn more about how to prove this with a couple of simple facts, look here: http://www.physlink.com/Education/AskExperts/ae535.cfm ). Suffice to say, the fact we have two main, noticeable, rotations we are experiencing at all times means there are certain considerations which need to be taken into account when creating a precise, universal system for measuring and plotting the observable skies.

First of all, we have the Earth’s rotation on its own axis which goes from the South Pole to the North Pole, which means there are portions of the 24 hour rotation when we can see the light of far off stars and galaxies (night), and a time when we cannot, i.e. the Sun is bright enough the during the day it outshines anything else. This is compounded on a 365 full on-axis rotation (day) long journey around the Sun, which means the stars we see change according to which part of our orbit we’re on (full view of this here: https://www.youtube.com/watch?v=R2lP146KA5A). This is also complicated by the fact the Earth’s axis is rotated slightly, which is the entire reason we have seasons of the year as one hemisphere of the Earth receives more light/energy than the other.

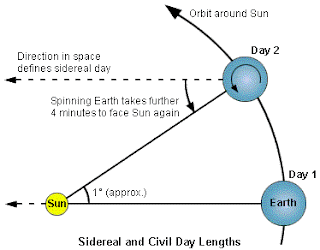
Altogether, this series of rotations and shifts causes a noticeable difference in how the sky we observe is consistently different day to day. This is due to how, let’s say, we wish to see a specific star and have it appear directly above the observer, at 90 degrees from the horizon, then when the Earth has moved \(\frac{1}{365}\) part of a circle, then there is additional rotation time needed in order for the star to be at the right position once again. Look here:  

This entire concept is known as Sidereal Time, and the adjustment made every day to account for this Sidereal Time shift is: \[Sidereal ~Time ~Shift = \frac{24~ hours \times 60 \frac{min}{hour}}{365 ~days}\] \[ Sidereal ~Time ~Shift = 4 \frac{min}{day},\] which means every Sidereal Day is 23 hours and 56 minutes long.

Furthermore, we have an additional concept called Local Sidereal Time (LST), which is the Right Ascension Hour (an actual time at which an object is on the stellar meridian (the line that intersects the Earth’s equator projected onto the stars at 90 degrees)). We add on the actual, physical hour of the present day to the shift accumulated since noon on the 20 of March (in the case of 2015), which is the Vernal Equinox, the day when the daytime and nighttime are the same length. This turns out to be:

a) Now, starting the problem, we want to find out the LST at midnight on the Vernal Equinox. Here, we know the time difference from noon to midnight is 12 hours, which corresponds to the \(H\) in the \[LST = H_{Hour~ Angle} + \alpha_{Right ~Ascension},\] and the LST shift for half a day is simply 2 minutes (half of 4 minutes), so the LST at midnight is just \[12:02 .\]

b) Letting time elapse for an additional 24 hours, we know a day is equal to 4 more minutes in LST, so on one day past the Vernal Equinox at midnight, the LST would be \[ 12:06 .\]   

c) Assuming we are defining “right now” as the first time we solved this problem, on Tuesday, February 2, 2016 at 3:00 pm, we can make some wide analyses to find the LST.

From the 2015 Vernal Equinox to February 2, 2016, 318 days have passed. For every day, the LST gains an additional 4 minutes on its shift from the current time. So, if we take the change in Right Ascension, which is the shift, \(\alpha\) :\[\alpha = 318 days \times 4 \frac{min}{day} \div 60 \frac{min}{hour} = 21.2 hours = 21:12 ,\] and we now add the 0.5 minute LST shift from the three hours that elapsed since noon, the final \( \alpha \) is \( 21: 13 \). Therefore, by adding the Hour Angle (H), \(3:00\), we have \[LST = \alpha + H \] \[LST_{Feb~ 2, ~ 2016,~ 3:00PM } = ~21:13~ + ~3:00 \] \[ LST_{Feb~ 2, ~ 2016,~ 3:00PM } = 0: 13 \approx 0:00.\]

d) Furthermore, by having the basis for February 2, at 3pm, it is only a matter of adjusting a bit more to have the LST for midnight on the same day. It is currently 3:00 pm, which means 9 more hours will elapse, and the corresponding LST shift would be 1.5 minutes \[ \frac{4}{24} = \frac{x}{9}\] \[x = 1.5,\] so the new time would be the addition of the shift and the actual hour change: \[ LST_{Midnight} = 0:16 + 9:00 + 0:02\] \[ LST_{Midnight} = 9:18 \approx 9:00 .\]

e) Undeerstanding the basic mechanics of LST, we can now use it to extrapolate it to other dates, like my birthday, October 7, on its sunset: 6:14 pm. So if the Vernal equinox this year is March 20, we start here with the 0:00 date. Now we add on the days from that day till my birthday, being:

\[11_{March} + 30_{April} + 31_{May} + 30_{June} +31_{July} + 31_{August} + 30_{September} + 7_{October} = 201 ~days\] \[ LST ~Shift = 201 ~days \times 4\frac{min}{day} = 804 min = 13:24 ,\]

And knowing the precise time of the sunset plus its shift since noon (approximately 1 minute), we have: \[LST_{Sunset} = 13:24 + 6:14 + 0:01 ,\] \[ LST_{Sunset} = 19:39 .\]

*Small disclaimer, my real birthday is a couple of days off from what we used here, but you know, identity theft is a thing in this world now.