Why aren’t stars perfect Blackbodies?

We are bounded in a nutshell of Infinite Space: Reading #2: Why aren’t stars perfect Blackbodies?

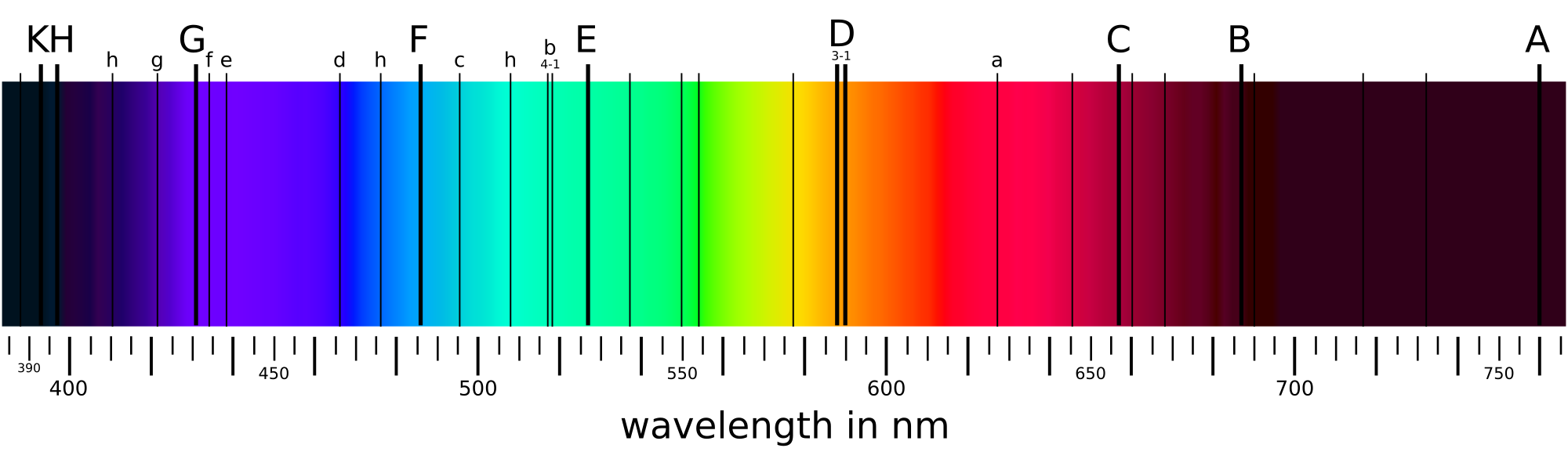
All this time, we have been explaining how stars are easily approximated as blackbodies, which offers us great insights into their properties. However, there is a condition which limits the possibility of establishing a sure connection between the theoretical approximation of a blackbody and a huge mass of nuclear fusion held together and pulled apart by gravity and pressure. These are the dips in a spectral image of a star:

So what is the source of these dips, for which we travel to the early nineteenth century, where spectral lines are about to be discovered. In 1802, William Wollaston was the first we know to have seen and describe the dark lines which appeared after splitting the light stemming from the Sun with a prism. Later on, Joseph Von Fraunhofer, a German optician, successfully split the spectral lines of the Sun and catalogued all 475 according to their width and position. These spectral lines are now known as Fraunhofer lines, and they were used to find the elements which compose the Sun.

While observing these lines, Fraunhofer was able to pick out the specific lines which make up the specific color of salt when thrown into a flame. Using this same technique, Robert Bunsen would create a burner which most precisely yielded the color spectrum of different elements when exposed to the flame. Along with Gustav Kirchhoff, Bunsen found how these specific lines in the Fraunhofer solar spectrum corresponded directly with the lines emitted by other elements, as is the case of iron and what would later be determined as Helium in 1868. Kirchhoff, being a theoretical physicist, established a set of descriptions to broadly explained spectral lines, the most relevant being how cool, diffuse gas could absorb energy from the full spectrum and create absorption lines.

These absorption lines also helped other scientists and astronomers find a clear relationship between slightly different spectra, caused by what we then learned was the phase shift from the Doppler effect of moving while emitting photons. This equation is described as: \[\frac{\lambda_{obs} - \lambda_{rest}}{\lambda_{rest}} = \frac{v_r}{c},\] where \(v_r\) is the radial velocity, c is the speed of light, and the wavelengths are differentiated form being the observed ones and the normally emitted. These early descriptions of moving objects would be the basis of Hubble’s expanding universe model, based on a shift in the wavelength of atomic hydrogen from the established standard, z, also known as redshift, is calculated precisely the same as the radial velocity is. Spectral lines are the basis for our understanding of what other objects are made of, and are what has allowed us to better see how other systems develop, accumulate matter, and how stars forge the heaviest elements in spectacular explosions we call supernovae. 

References: 

Maoz, D. Astrophysics in a Nutshell.

Carrol & Ostlie; 2007; Introduction to Modern Astrophysics

https://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Fraunhofer_lines.svg/2000px-Fraunhofer_lines.svg.png